Our research group focuses on Calculus of Variations which is a set of theories based on the fundamental works by Bernoulli, Euler, Lagrange, and Weierstrass. More and more problems arising from Applied Mathematics, Economics and Engineering, but also from real life, have been studied by models in calculus of variations. Typical problems concern the optimization of a functional (often of integral type) that has to be minimized/maximized or they are formulated in terms of ordinary and partial differential equations with a variational structure. Some questions arising in applications lead to variational models with non-standard growth conditions. Relevant examples are in elasticity theory and material sciences to model strongly anisotropic materials, such as composite and biological materials. In this type of models the local regularity of minimizers has been widely studied in recent years, but several  questions still remain open. Another type of optimization problems consists in minimizing an energy functional depending on a shape which varies in a suitable class of admissible choices. An example consists in rigidifying a membrane fixed at its boundary, under the action of an exterior load. A stronger membrane can be obtained by adding a one-dimensional reinforcement in the most efficient way. Other models, based on the Total Variation, have been employed in a wide variety of image restoration problems, quickly becoming one of the most active research topics in image processing and computer vision. The most basic image restoration problem is denoising, that is, preserving the most significant features of an image while removing the noise. The approximation of the total variation (in the isotropic and anisotropic variants) by non-local functionals have been studied recently by several authors and lead to new and more efficient models.

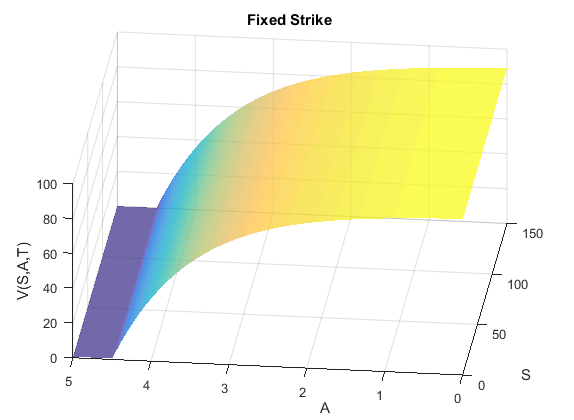
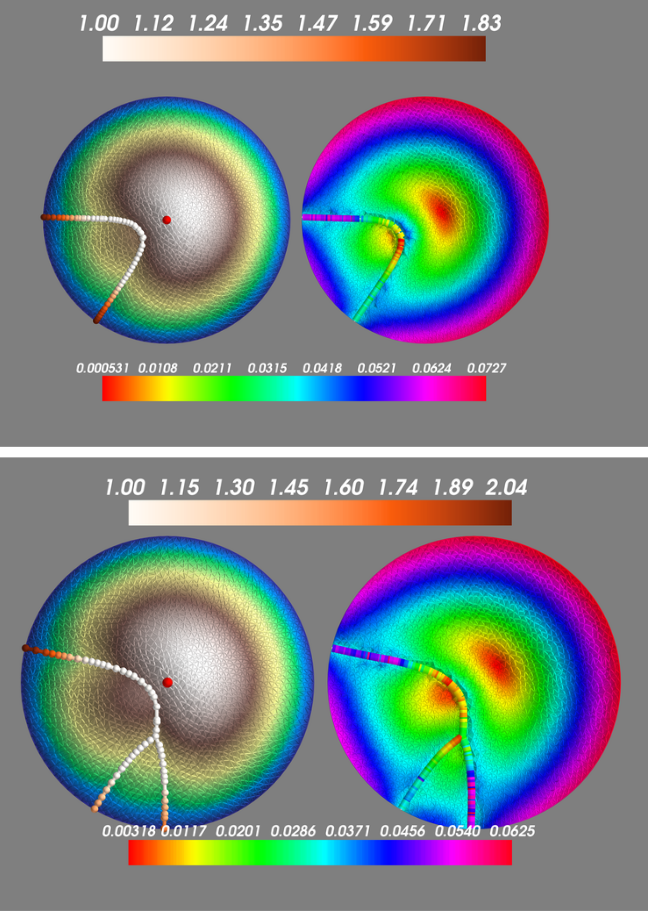
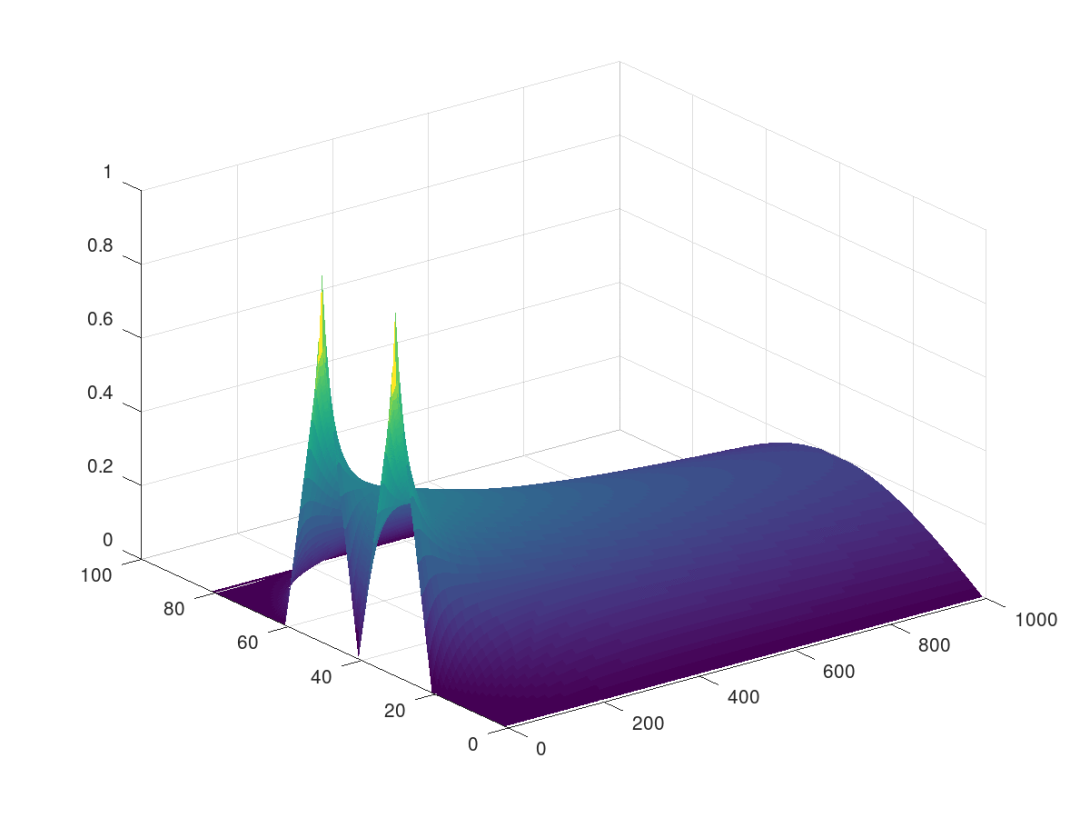
The Black & Scholes theory applies to more general contingent claims, including the Asian options. The relevant Kolmogorov equation is strongly degenerate and requires the development of an “ad hoc” regularity theory for its treatment and for the development of its numerical analysis. A challenge of the research team in this field is the regularity theory for the obstacle problem, which arises in the study of part-dependent American options.

A related goal is to provide solutions to the modelling of the asymmetry of risk in financial markets. There is increasing empirical evidence that classical financial models are not fully adequate and hould be pushed beyond their current limitations. A specific challenge is to capture skewness (directional asymmetry) in return distributions.

The Black & Scholes model relies on the stochastic theory to describe the financial markets in order to deal with the problem of hedging and pricing of European options. The so called Black & Scholes formula provides us with the fair price of an European option, and is widely used to compute the implied volatility of the Stock market.

Nonlinear evolution models arise in several areas, like quantum Physics and phase-transition phenomena. The nonlinear feature of the equations, sometimes very strong, is due to the total or partial avoidance of linearization procedures. These, on the one hand, make the analytical problem more treatable while, on the other hand, decrease its efficacy since the model is a good approximation of the physical or chemical phenomenon only for a small range of data. Non-isothermal models became recently very interesting, in particular as far as existence, uniqueness and regularity of solutions are concerned. The physical consistency of the model may possibly lead to include singular potentials in the equations, like Dirac Delta or logarithmic free-energy potential, as well as dynamic boundary conditions. As a consequence, the mathematical analysis of the model is difficult from the very beginning, that is, from the local in time existence of a (weak) solution: this is the case in diffuse interface models, especially due to the coupling with the Navier-Stokes equations. Once this obstacle is overcome, the analysis of the longterm dynamics can be addressed. From this point of view, the knowledge of stationary states and bifurcation phenomena is relevant. In a more global perspective, when energy, heat or other type of dissipation occurs, one may try to devise a properly small set which at the same time represents the longterm dynamics, called global attractor.

The existence and uniqueness of the solution to the most important partial differential equations is often proved in some “weak sense” by general theoretical theorems of functional analysis. The regularity theory aims at proving that the weak solutions are actually smooth enough to satisfy the partial differential equations exactly the way that it is posed. It involves a broad variety of isolated issues including the Sobolev and Morrey embeddings, the Schauder estimates, the Harnack estimates, the blow-up methods.
The research team studies several families of partial differential equations, including evolution equations modeling physical phenomena, Kolmogorov equations, kinetic equations, Hörmander operators, equations arising in variational problems, obstacle problems.

Elliptic partial differential equations (PDEs) arise from multiple contexts in the Mathematical Sciences, and are key to understand and model natural phenomena, from the study of equilibrium capillary surfaces to the stability of quantum and stellar systems.

Our research interests cover PDEs which involve various differential operators both on bounded and unbounded domains: the Laplacian, the biharmonic and higher order Laplacian operators, the p-Laplacian, and the fractional Laplacian. For most of the equations, we are interested in understanding the existence and qualitative features of the solutions, comprising regularity, symmetry, symmetry breaking, decay and sign properties.

A broad class of equations we consider are either nonlinear or nonlocal, and possess a variational formulation. The starting point in the analysis of new problems with a variational structure is to provide a suitable environment (functional space) for the related energy. This often requires the study of new functional spaces and embedding inequalities, in the spirit of Sobolev, Moser, Trudinger, Adams, Gagliardo, Nirenberg and Strauss. Besides applications to variational PDEs, establishing sharp (not furthermore improvable) versions of such inequalities turns out to be relevant also from a pure theoretical point of view, and opens the way to additional lines of research concerning optimal constants and the existence of optimizers.

Recurrent nonlinearities in our equations are “critical” with respect to the embedding properties of Sobolev into Lebesgue spaces. The interest for equations with critical nonlinear terms has been triggered in the past by the pioneering works of giants like Brézis and Nirenberg, which still inspire researchers worldwide. Typically these nonlinearities have either polynomial or exponential critical growth, and produce loss of compactness and energy quantisation phenomena for the sequences of approximated critical points of suitable functionals.

In this context a careful compactness analysis is performed by means of new Liouville-type theorems, yielding existence and multiplicity results. This is often obtained by reviewing tools within the infinite dimensional Morse and the Lusternik–Schnirelmann theories, for example by variants of the Mountain-Pass theorem of Ambrosetti and Rabinowitz.

For equations set on unbounded domains, we are also interested in the asymptotic behavior of the solutions, by means of variational and perturbation methods, e.g. either by the Lyapunov–Schmidt reduction or by estimates based on the maximum principles. For equations set on bounded domains, our research includes the study of asymptotic properties of the spectrum of the Laplacian with Dirichlet boundary conditions.