A group of researchers has a sound tradition in the study of algebraic and geometric structures, which are either discrete or can suitably be treated through discretization techniques: The study of such topics embraces themes of great interest for their applications to science and technology. For instance, graphs are employed nowadays within the most common data structures and computing algorithms, and can even be encountered in the study of social and financial phenomena; knot theory is connected with the study of biological structures (comparison of genetic data) and physical structures (string theory); computational topology has become a basic tool for the computer guided description and comparison of shapes, with a subsequent fallout on graphic manipulation, on the comparison of models and on the acquisition of visual information. A good amount of experience was gained in enumerative problems from various contexts, developed on different platforms, which is susceptible of further growth.
The three main areas of investigation are the following:
Algebraic and differential topology
- Topology and geometry of manifolds
- Combinatorial group theory
- Algebraic topology, homological algebra and L-theory
Applications of crystallization theory to geometric topology and quantum gravity
- Relations between crystallization theory and colored tensor models in quantum gravity
- Trisections of PL 4-manifolds with boundary
- Generation of catalogs of PL 4-manifolds using colored graphs and their classification
Discrete mathematics
- Graph coloring, decomposition and characterization
- Matching search, perfect matchings (1-factors), 2-factors
- Graph theory techniques applied to DNA assembly problems
Staff researchers:
Cristina Acciarri, Arrigo Bonisoli, Simona Bonvicini, Maria Rita Casali, Alberto Cavicchioli, Paola Cristofori, Camilla Felisetti, Giuseppe Mazzuoccolo, Fulvia Spaggiari, Giovanni Zini
The scientific research principally regards problems related to topological and differentiable manifolds (and their generalizations) faced by techniques of Algebraic, Geometric and Differential Geometry, Combinatorial Theory of Groups, Homological Algebra, Knot Theory, and Graph Theory. The main goals of the research are to obtain the topological and homotopical classification of large classes of spaces (as manifolds, generalized manifolds, Poincare` complexes, structured polyhedra, etc.), to determine the cobordism class of them and to compute their principal algebraic invariants. Using methods of Homological Algebra and L-Theory, we study several questions of Algebraic Surgery Theory on compact manifolds and of Dehn-Lickorish Surgery on knots and links. We also analyze the algebraic properties of the obstruction groups for Surgery and construct several spectral sequences which are very useful for the classification problems mentioned before. Finally, the representation of compact polyhedra by means of oriented and/or coloured graphs allows us to give combinatorial methods for the explicit computation of their algebraic and numerical invariants.
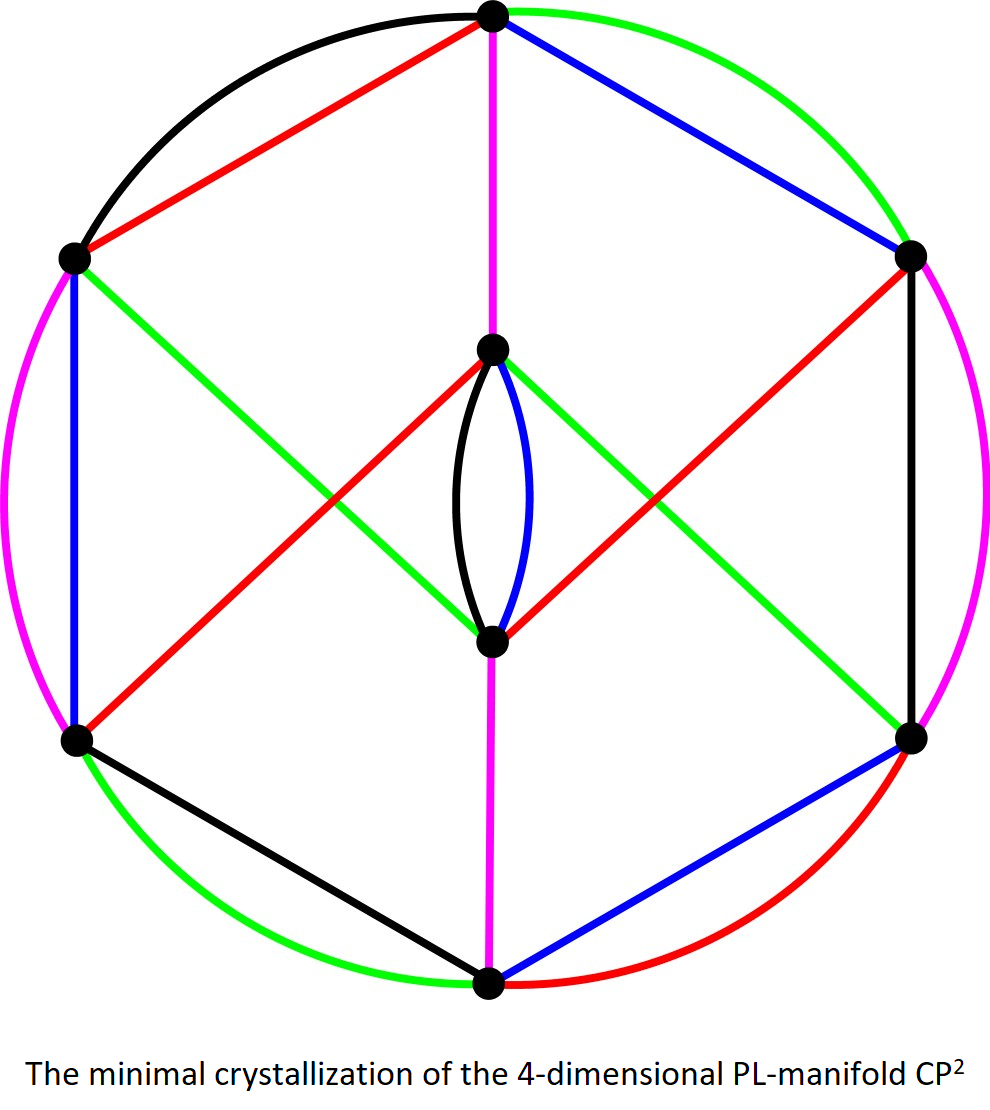
Crystallization theory is a graph-theoretical representation method for compact PL-manifolds of arbitrary dimension, with or without boundary, which makes use of a particular class of edge-coloured graphs, which are dual to coloured (pseudo-) triangulations. These graphs are usually called gems, i.e. Graph Encoding Manifolds. One of the principal features of crystallization theory relies on the purely combinatorial nature of the representing objects, which makes them particularly suitable for computer manipulation.
Recent research by the local group focuses on:
- relationships between crystallization theory and coloured tensor models in high dimensional quantum gravity
- generation of catalogues of PL-manifolds for increasing values of the vertex number of the representing graphs, both in dimension three and four
- definition and/or computation of invariants for PL-manifolds, directly from the representing graphs, in dimension n ? 3
- trisections of PL 4-manifolds with boundary
Finite geometry deals with geometric structures consisting of finitely many objects. Most of them can be described by the notion of a block-design consisting of a finite set of points and a collection of subsets of the point-set called blocks. The relevant geometric properties derive from the incidence relations which are imposed on the structure under consideration. Finite geometry includes the study of finite projective and affine spaces, in particular projective and affine planes (whose non-desarguesian models are far from being classified), and the so called circle-geometries (Möbius, Laguerre and Minkowski planes) that generalize the geometry of quadrics in 3-space. In recent years increasing interest has been devoted to the notion of a graph-design, that is a block-design in which each block has the "shape" of an assigned graph.
Structural properties of specified classes of graphs may well be of interest in their own right and so when adopting this point of view graphs become THE object to be investigated rather than forming a model for studying something else. So, for instance, the class of graphs admitting a Hamiltonian cycle is not yet fully understood. This area of discrete mathematics is famous for many problems admitting an elementary formulation but whose solution is not elementary at all: the 4-colour theorem is perhaps the most famous instance in this respect. As a matter of fact many conjectures in Graph Theory are still wide open and progress is slow. The study of large examples or putative counterexamples may well involve enumerative arguments and the use of computer techniques. Current research often involves graphs which are nowadays known as “snarks” (they are essentially cubic graphs not admitting a 3-edge-colouring).